Many investors confuse the terms ‘risk’ and ‘uncertainty’. At first glance this does not seem a big deal, but a closer look will show that they are two fundamentally different things. Approximately 100 years ago, Frank Knight wrote in his book "Risk, Uncertainty and Profit" that the terms ‘risk’ and ‘uncertainty’ are not neatly separated:
"Uncertainty must be understood in a sense radically different from the familiar concept of risk. [...] Measurable uncertainty or actual 'risk' is so different from unmeasurable uncertainty that it is really not uncertainty at all." [1]
Let us look closer at his statements;
Risk
Knight's statement clarifies what makes the crucial difference: risk is quantifiable. This is true, for example, when conducting random experiments or participating in games of chance. Here, probabilities and times for success or failure as well as the consequences of action and all possible scenarios are known and thus predictable. Or let us think of the calculation of insurance policies, where the whole thing can at least be estimated with high degrees of accuracy, whether logically or empirically. Therefore, good decisions under risk require above all logic and statistical thinking.
Uncertainty
Unlike risk, uncertainty is not quantifiable. This is due to the influence of unknown or incomplete information as well as the fact that investors need a certain amount of time to correctly assess certain probabilities. Let's think of the Corona crisis in spring 2020, which was thought possible in advance but not seriously considered. Political developments such as Brexit or the intervention of the Chinese government in the markets are also characterised by uncertainty. In these cases, only woolly or subjective assessments can be made. Therefore, good decisions under uncertainty conditions require intelligent heuristics and also intuition. Another solution is systematic, forecast-free strategies that have clear rules for limiting losses from the outset.
Structural breaks
One problem in the markets is that risks are quantifiable, but they are not constant like in a dice game - they keep changing and thus create uncertainty as to whether an approach will still have an advantage in the future. This is why there are only a few permanently stable strategies.
Let's assume that a trading approach has a hit rate of 65 percent and a payoff ratio of 1.0 in the backtest. It is therefore a profitable strategy. And if there were only risk, one could "safely" earn money with it. However, the decisive factor here is that there is always the added uncertainty of whether these values are even (approximately) correct for the future.
The following graph illustrates this: After 250 observations, there is a 50 percent probability of a structural break. The problem is to detect the break as quickly and as reliably as possible.
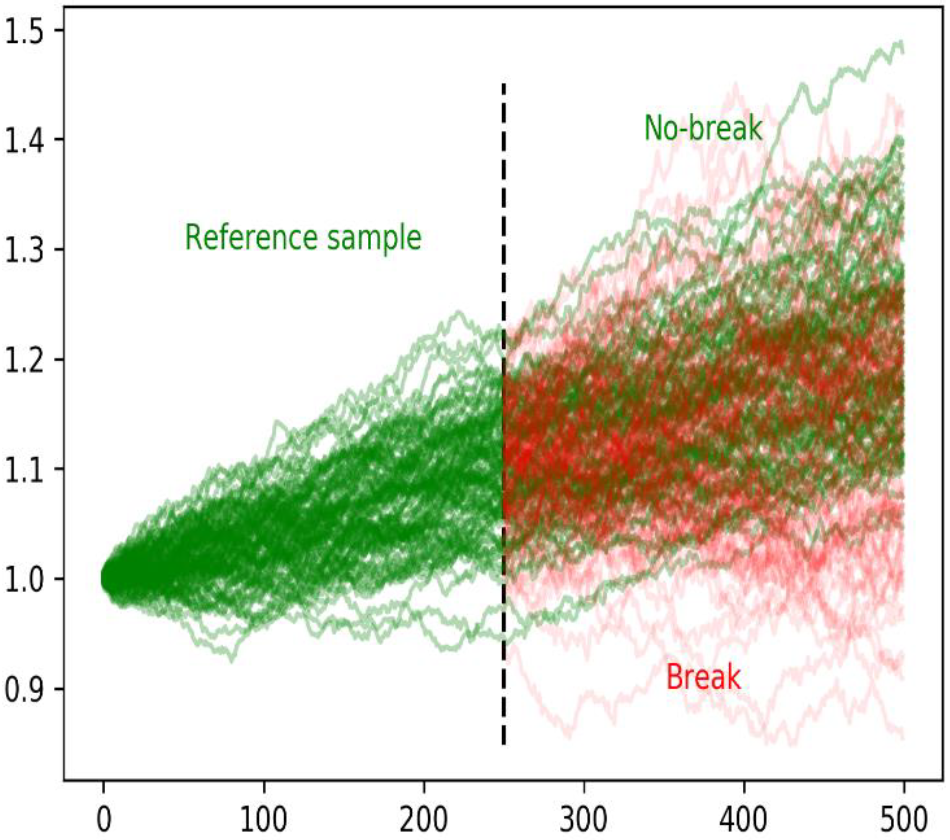
Source: de Prado, M. L (2021), Escaping The Sisyphean Trap: How Quants Can Achieve Their Full Potential, p. 9
The knowledge matrix
Besides the question of quantifiability, it also depends on what we know and what we don't know, and how aware we are of these things. In this regard, former US Secretary of Defence Donald Rumsfeld formulated a well-known saying at a press conference on 12 February 2002:
"There are things we know we know. We also know there are unknowns; that is, we know there are some things we don't know. But there are also unknown unknowns - those are the things we don't know we don't know." [3]
From these concepts, the following matrix can be created to structure strategic action in a meaningful way.
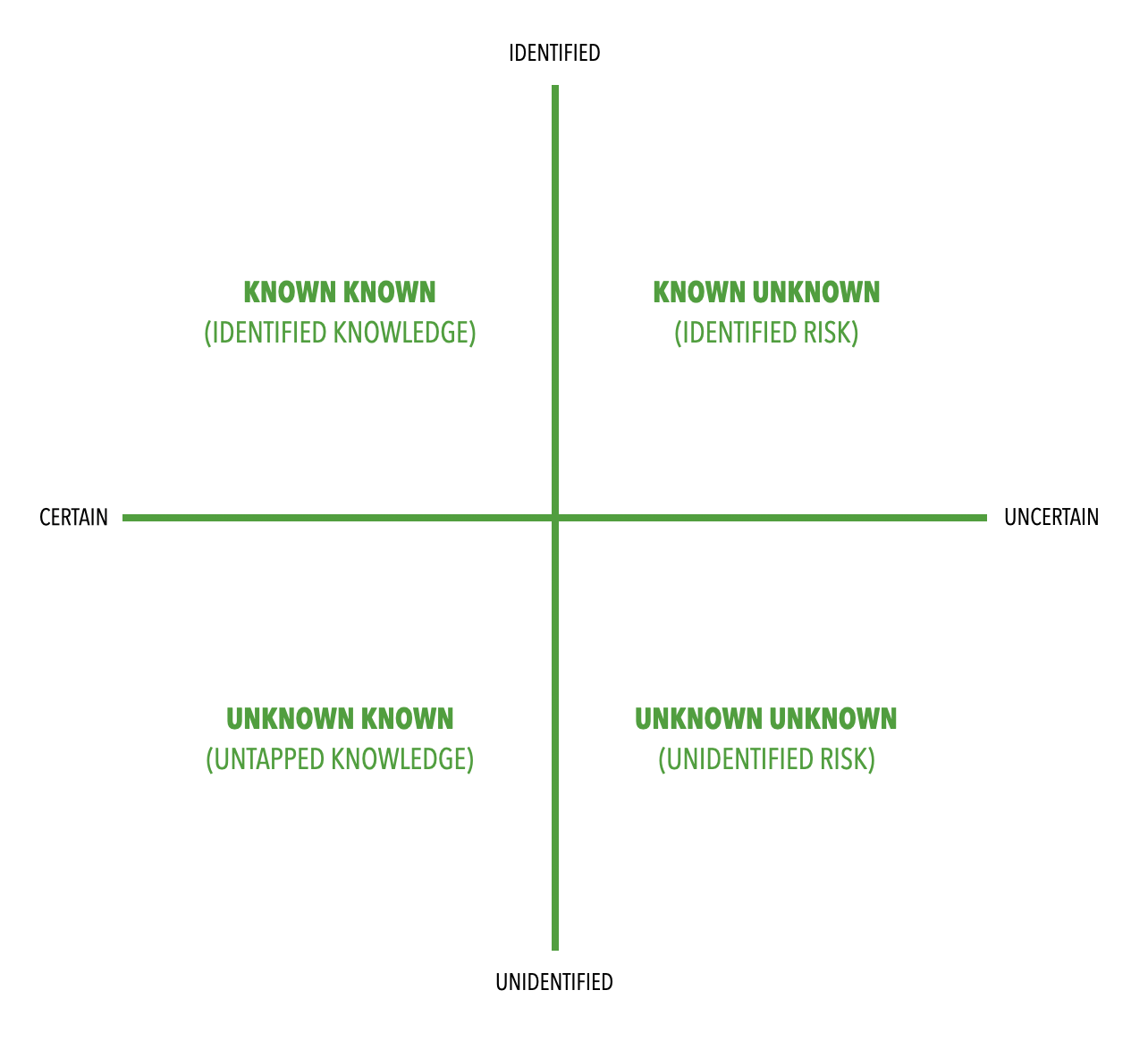
Source: Brier, N. (2020), Why is this interesting? - The Known Unknowns Edition, https://whyisthisinteresting.substack.com/p/why-is-this-interesting-the-known, accessed on 04.10.2021.
Known Knowns are cause-effect relationships that we know and know how to deal with (on a daily basis).
Unknown Knowns are statistical forecasts of events, such as error rates or voter turnout, whose occurrence and extent can be predicted relatively accurately for larger numbers of events, but not exactly for individual cases.
And Known Unknowns describe known gaps in knowledge in the sense of deliberate ignorance that can be reduced through questions and research. [3]
Unknown Unknowns, on the other hand, catch us completely off guard: They are events or coincidences that surprise us in their nature, scope and impact. Particularly severe Unknown Unknowns are also known as Black Swans - extremely rare, unpredictable events that have a significant impact on markets. [5] By definition, an Unknown Unknown transforms into a Known Unknown with its first occurrence, may subsequently become an
Unknown Known through empirical analysis, and may later become a Known Known. [3]
A paradox
Black Swans, however, give uncertainty an overly negative slant. In practice, it can just as well be understood in a positive light, in that there is potential for pleasant surprises, for example. And anyway: investors expose themselves to risks and uncertainties precisely because they expect a positive return from them in the end.
However, many people have a certain fear of uncertainty, as can be shown by the Ellsberg Paradox. [6] Suppose there are two urns, each containing 100 balls:
- Urn 1 contains 50 red and 50 black balls.
- Urn 2 contains 100 balls (still red and black). It can contain any combination.
First, the player chooses whether red or black means a win. Then a ball is drawn at random from one of the urns. Which would be better for this, urn 1 or urn 2?
The most common answer is that urn 1 is preferred. This is paradoxical: because no matter which colour was chosen before, it is assumed that a 50/50 chance is better than a completely uncertain distribution. But it cannot be that drawing both a red and a black ball from urn 1 is statistically better than drawing from urn 2 with any distribution.
If you are indifferent between red and black, from a statistical point of view you cannot do worse with urn 2. And yet we shy away from choosing the uncertain urn and prefer to take the risky one. We prefer the known risk, even though it brings no advantage.
What is often forgotten or underestimated in uncertain situations is the chance that our result could also turn out better than expected. The chance that there are almost only red balls in urn 2. Or the chance that a share will rise 100 percent instead of ten percent.













