The Experiment
The coin toss experiment is described by Victor Haghani and Richard Dewey in their paper "Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin". [1] Haghani is well known in the financial industry: He was one of the founding partners of the now-failed hedge fund LTCM.
Before the start of the game, the 61 participants were given a clear indication that the simulated coin had a 60 percent probability of heads and a 40 percent probability of tails. The starting capital was 25 US dollars each. It was explained that the balance would be paid out at the end of the game subject to a maximum amount. The maximum was 250 US dollars and was only communicated to the players when they reached this amount in order not to distort the previous expectation.
The results
The participants in the experiment were mostly economics students and young professionals from financial companies. One could therefore assume that they should be well prepared to play a simple game with fixed positive expectations. But the results had a surprise in store for them.
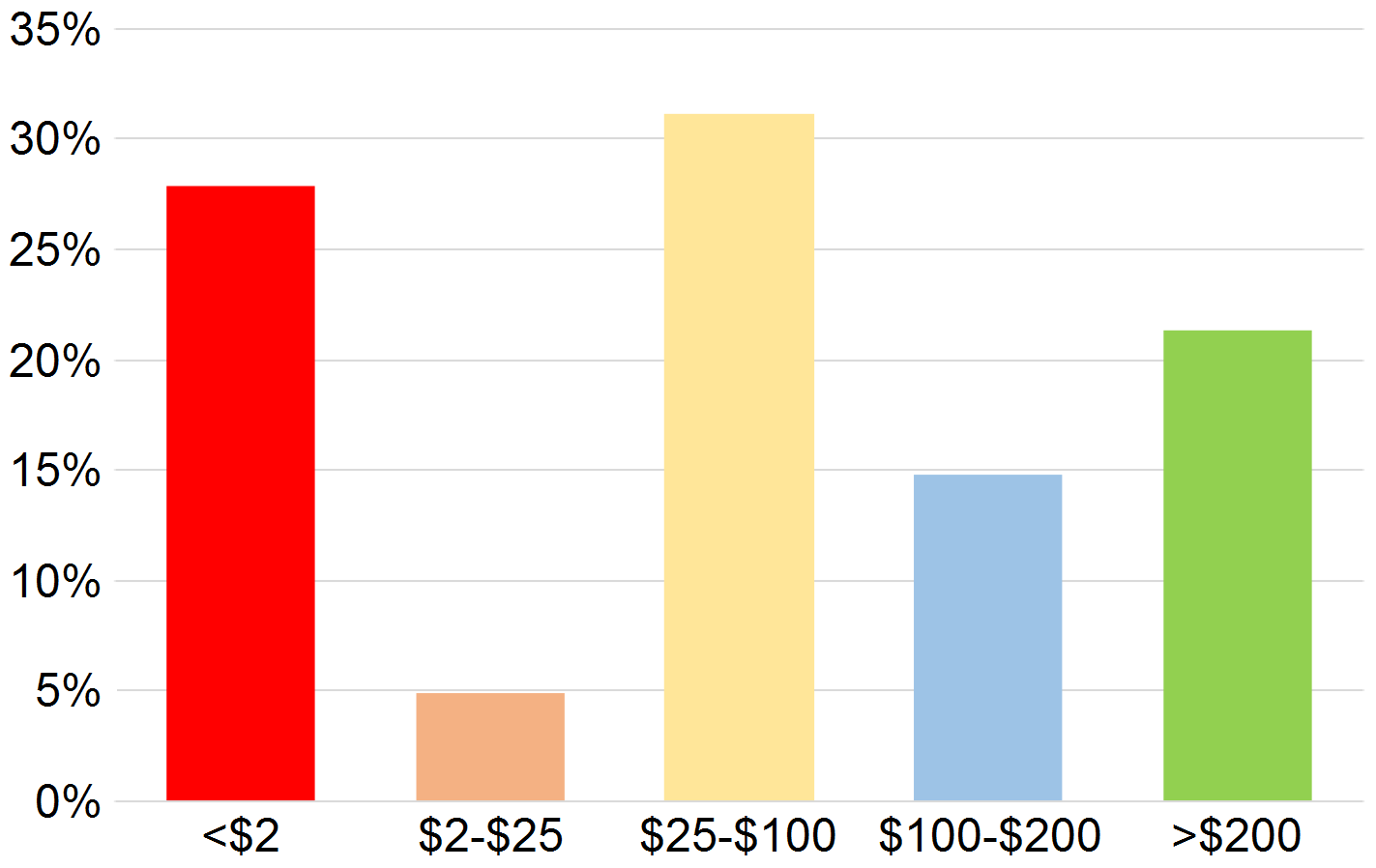
The graph shows the distribution of the final assets after 30 minutes of playing time. Roughly speaking, three categories can be distinguished: Gamblers (left in red), conservatives (centre in yellow) and strategists with optimal betting behaviour (right in green).
Source: Haghani, V. / Dewey, R. (2016), Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin, p. 4
The participants placed suboptimal bets in all shapes and sizes: too high or too low, and showed erratic betting behaviour irrationaly betting on tails instead of heads. In this way, most of them gambled away their chance to go home with 250 dollars after half an hour of play. In fact, only 21 percent of the participants reached this maximum. But even more astonishing was the fact that 28 percent of the participants went almost or completely bankrupt (residual value below 2 dollars).
„If you gave an investor the next day′s news 24 hours in advance, he would go bust in less than a year.“ (Nassim Taleb)
Even from a purely intuitive perspective there seems to be an optimal betting strategy in this game. If the risk is too high, you run the risk of losing so much money on a series of number throws that you can't recover from it. On the other hand, if the percentage at risk is too low, you do not make the most of the temporary opportunity to place bets with a statistical advantage.













